Come calcolare l’area di una nuvola (e la magia dell’infinito)

La nuvola, la regina delle forme irregolari

Immaginiamo una nuvola: è, per definizione, la regina delle figure irregolari.
Supponiamo di volerne calcolare l’area, cioè misurare la superficie che occupa in cielo.

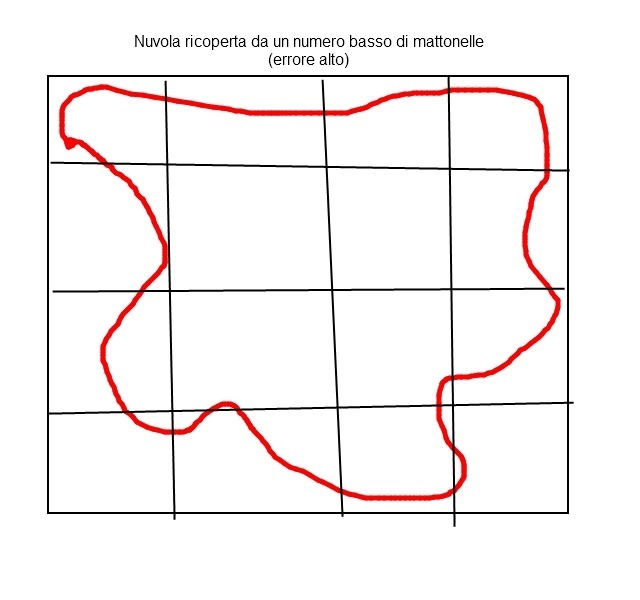
Un buon metodo è ricoprire l’intera nuvola con una serie di mattonelle quadrate la cui area è nota, ipotizziamo di un metro quadro.
Se riuscissimo a foderare la nuvola utilizzando – ad esempio 50 mattonelle – potremmo affermare che l’area della nuvola vale, più o meno 50 metri quadrati.

L’errore dipende dal numero di mattonelle

La stima è imprecisa: l’errore che si commette è dovuto all’approssimare l’area della nuvola (di forma irregolare) come somma di aree di figure regolari (le mattonelle quadrate).

La differenza (lo scarto) diminuisce se utilizziamo piastrelle di dimensioni minori che, però, implica incrementare il numero di elementi da usare.
L’errore, quindi, dipende dal numero di piastrelle a disposizione: esso tende a zero (ma in realtà non è mai nullo) con l’aumentare della quantità di mattonelle.

E se usassimo infiniti granelli di sabbia?

La sfida è avvincente e desideriamo migliorare la stima: passiamo dalle mattonelle a piccoli granelli di sabbia.
Supponiamo che sia nota l’area del singolo e microscopico granello di sabbia (ad esempio, un millimetro quadrato): con un po’ di impegno, riusciamo a rivestire l’intera nuvola (anche nei contorni) con una certa precisione con un numero altissimo di chicchi (altissimo ma sempre finito!).

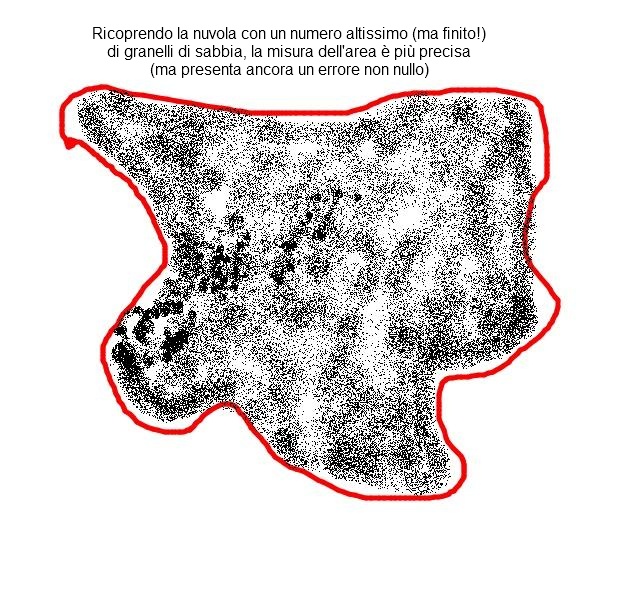
Più alto sarà questo numero, più precisa sarà la nostra misurazione, minore sarà l’errore che si commetterà nell’approssimare l’area della nuvola come sommatoria di arie infinitesimali.
Se – per assurdo – avessimo a disposizione un numero INFINITO di granelli di sabbia, potremmo ricoprire l’intera superficie della nuvola in modo uniforme, senza “buchi” e calcolare precisamente la sua area come somma di infinite aree: tale misurazione sarebbe esatta con errore zero.

Il limite, magia dell’Analisi Matematica

Il paradosso è servito: nella realtà non abbiamo a disposizione l’infinito, ci dobbiamo accontentare dei “miliardi” che – seppure siano un valore illimitato – è pur sempre finito, cioè possibile da contare (in teoria).

Per nostra fortuna, il mondo Matematico, a differenza di quanto si immagini, è magico e fantasioso e tutto diventa possibile, anche toccare con mano l’orizzonte.
Lo strumento che ci permette di raggiungere il confine tra terra e mare è appunto IL LIMITE.

Per chi desidera sognare, consiglio la lettura della favola di Tau il Topologo.

Commenta via facebook

Commenti